Główka pinezki ma powierzchnię ok.
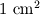 , a koniec jej ostrza — ok.
, a koniec jej ostrza — ok.
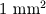 . Jakie ciśnienie wywierasz na główkę pinezki, gdy działasz na nią siłą
. Jakie ciśnienie wywierasz na główkę pinezki, gdy działasz na nią siłą
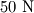 ? Jakie ciśnienie wywierane jest na powierzchnię, w którą wbijasz pinezkę?
? Jakie ciśnienie wywierane jest na powierzchnię, w którą wbijasz pinezkę?
Zadania
Ciśnienie:
Przykład:
Główka pinezki ma powierzchnię ok.
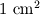 , a koniec jej ostrza — ok.
, a koniec jej ostrza — ok.
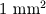 . Jakie ciśnienie wywierasz na główkę pinezki, gdy działasz na nią siłą
. Jakie ciśnienie wywierasz na główkę pinezki, gdy działasz na nią siłą
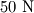 ? Jakie ciśnienie wywierane jest na powierzchnię, w którą wbijasz pinezkę?
? Jakie ciśnienie wywierane jest na powierzchnię, w którą wbijasz pinezkę?
Rozwiązanie:
Ciśnienie wywierane na główkę pinezki wynosi:
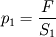
gdzie F = 50N, a S1 = 1cm2 = 0,0001m2.
Podstawiając wartości liczbowe, otrzymujemy:
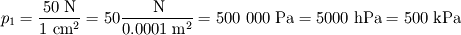
Ciśnienie wywierane przez pinezkę na powierzchnię, w którą jest ona wbijana, wynosi natomiast:
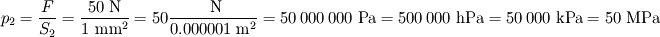
Jak widzisz, pinezkę można potraktować jak „wzmacniacz ciśnienia” (patrz rysunek).
Ciśnienie hydrostatyczne i prawo Pascala:
Zastanów się, jakie ciśnienie panuje na pewnej głębokości pod wodą. Wykorzystaj do tego celu naczynie o polu podstawy S. Tym, co wywiera ciśnienie, jest woda znajdująca się powyżej. Ma ona pewien ciężar i przez to wywiera nacisk na podstawę.
Ciężar wody znajdującej się w naczyniu wynosi:
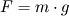
gdzie m — to masa wody, a g — to przyspieszenie ziemskie.
Znając gęstość ρ i objętość V wody, możemy wyznaczyć jej masę:
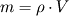
Objętość wody znajdującej się w naczyniu, to pole podstawy S pomnożone przez wysokość h:
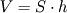
Ciśnienie, które woda wywiera na dno naczynia, jest równe:
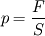
podstawiając wyprowadzone wyżej wyrażenia na F, m i V:
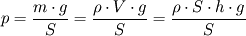
i skracając S w liczniku i mianowniku, otrzymujemy:
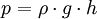
Zastosowanie prawa Pascala:
Przykład:
Rozwiązanie:
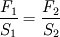
Największa przyłożona siła F1 = 250N,
pole powierzchni mniejszego tłoka S1 = 100cm2,
pole powierzchni większego tłoka S2 = 900cm2.
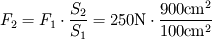
Największa siła, jaką możemy uzyskać, jest więc równa:
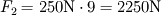
Jaką masę można podnieść za pomocą takiej siły?
Aby podnieść ciało o masie m, należy zrównoważyć działającą na nie siłę ciężkości Fc równą:
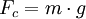 :
:
stąd:
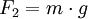
Dzieląc obie strony równania przez g, otrzymujemy:
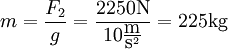
Ciśnienie atmosferyczne:
Przykład:
Rozwiązanie:
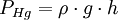
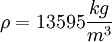 ,
, 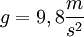 ,
, 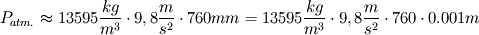
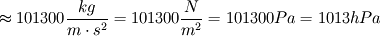
Siła wyporu:
Na każde ciało zanurzone w cieczy działają dwie siły — siła ciężkości
i siła wyporu. Od tego, która z nich jest większa, zależy to, czy ciało
będzie pływać, czy zatonie. Siła wyporu równa jest ciężarowi wypartej
cieczy:
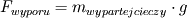
Siła ciężkości wynosi:
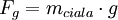
Masa ciała równa jest jego gęstości pomnożonej przez objętość, więc:
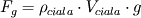
Objętość wypartej cieczy równa jest objętości zanurzonej części ciała — Vzan., zatem:
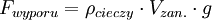
Jeśli chcemy, aby ciało pływało, to siła wyporu musi być większa od siły ciążenia:
czyli:
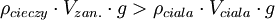
Po skróceniu wspólnego czynnika po obu stronach równania, otrzymujemy następujący warunek:
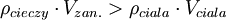
Gdy całkowicie zanurzymy ciało, to Vzan. = Vciala, a nasz warunek możemy uprościć: